Yay - first blog post of the year 2023!
We start with the basics of secret sharing before diving into more exotic stuff. The aim is cover the basics in this post and dive into [CDI05] or [Maurer02] in the coming weeks.
Motivation
Inspired by Oded Goldreich’s My Choices1, I have decided to kick the year off by researching some papers that I have never fully dug into but I have seen referenced countless of times during my research. However, to fully appreciate the specific techniques employed, we will in this post revisit some basic concepts.
Basics
Disclaimer: You should not be reading the following; you should first/instead visit Beimel’s timeless survey on Secret Sharing Schemes.
Before looking at LSSS we need to talk about access structures. These are important because they define which sets of parties in the system that together can access the secret.
Access Structures
Let $\mathcal{P}={\mathsf{P}_1,\ldots,\mathsf{P}_n}$ be the set of parties. An access structure $\Gamma$ has the following properties
- $\Gamma\subseteq 2^{\mathcal{P}}$ i.e. it is a subset of the power-set over all parties.
- $\Gamma$ is monotone meaning if $B\in\Gamma$ and $B\subseteq C$ then $C\in\Gamma$
We call sets in $\Gamma$ qualified sets while the members of $\Sigma=2^{\mathcal{P}}\setminus \Gamma$ (secrecy structure) are unqualified. Indeed, the monotonicity property essentially means that if set of parties are qualified then any super-set is also qualified. Conversely, if a set of parties is unqualified then any subset should also be unqualified.
Threshold Access Structures
A special case is the simple $t$-out-of-$n$ access structure $\Gamma_{t,n}$ where any subset of size greater than $t$ collectively have access to the secret. $\Gamma_{t,n}=\{A\subseteq 2^{\mathcal{P}}:|A|>t\}$.
Secret Sharing Schemes
A secret sharing scheme $\Pi$ consist of a sharing algorithm $\mathsf{Share}$ which takes as input a secret $s$ in some secret space $\mathcal{K}$ and some random string $r$ sampled from domain $R$ according to some prescribed distribution and outputs shares in $\mathcal{K}_1\times\dots\times\mathcal{K}_n$. Conversely, the reconstruction algorithm for a qualified set $A\in\Gamma$ can be written as a function $\mathsf{Recon}_A:\mathcal{K}_1\times\dots\times\mathcal{K}_n\rightarrow \mathcal{K}$. Very informally, correctness of $\Pi$ guarantees that any qualified set can collectively, by using the shares dealt by $\mathsf{Share}$, obtain $s$ by applying $\mathsf{Recon}$. While, security claims that to any unqualified set, all values of $s$ are equiprobable in $\mathcal{K}$.
Linear Secret Sharing
LSSS is a special class of secret sharing schemes based on linear algebra. In short, these schemes are based on an underlying finite field $\mathbb{F}$ such that both the secret space, share space and the randomness are related to $\mathbb{F}$. Importantly, we let the random string $r$ be a vector where each coordinate is an independent and uniformly chosen element in $\mathbb{F}$ such that $\mathsf{Share}$ is now a fixed linear function combining the secret $s$ and $r$ and outputting the shares.
LSSS and Minimal Span Programs...
The study of minimum share size necessary while keeping efficient (time polynomial in the number of parties $n$) $\mathsf{Share}$ and $\mathsf{Recon}$ algorithms is related to a concept in complexity theory called Monotone Span Programs (MSP). In fact, an MSP for specific access structure $\Gamma$ implies a linear secret sharing scheme for the same access structure [KW93]. This relationship is used to show relatively strong lower bounds on the information ratio (share size) for LSSS where the corresponding lower bounds proved for general access structures are seemingly weaker.
Shamir’s Secret Sharing
The most famous secret sharing scheme is arguably Shamir’s secret sharing. The concept was introduced independently by both [Shamir79] and [Blakley79]. The scheme is limited to threshold access structures $\Gamma_{t,n}$. This is a fairly well-known scheme so we will describe it briefly:
- $\mathsf{Share}$. Sample a polynomial $P\in \mathbb{F}[X]$ uniformly random subject to $P(0)=s$ and deg$(P)=t$ the resulting share vector is $(P(\alpha_1),\ldots,P(\alpha_n))\in\mathbb{F}^n$ where $\alpha_1,\ldots,\alpha_n$ are public predefined values.
- $\mathsf{Recon}$. Simply, do Lagrange’s interpolation on shares from the qualified set $A$.
Security comes from the fact that any $t$ unique points on the polynomomial (from an unqualified set) will render all values of $s$ equiprobable, while correctness ensures that any set of $t+1$ shares (qualified set) uniquely defines the polynomial $P$ and hence also $P(0)=s$.
Cheesy Tip. Shamir’s secret sharing is a testament to the fact that the threshold access structures $\Gamma_{t,n}$ are ideal. Essentially, this means that the individual share size is optimal and equal to size of the secret.
CNF Secret Sharing
The concept of secret sharing for general access structures was first put forth by [ISN89] and generalized to access structured described by monotone formulae by [BL90] who also showed that access structures described by small monotone formulae admits an efficient perfect secret sharing scheme.
The scheme for realizing secret sharing for general access structures are often referred to as CNF secret sharing2 or replicated secret sharing because the same values appears in multiple shares. First consider the maximal sets of the unqualified sets $\Sigma$. We can enumerate them as $\mathcal{T}={T_1,\ldots,T_k}$.
- $\mathsf{Share}$. To share a secret $s\in \mathbb{F}$, first sample $\lbrace r_T\rbrace_{T\in \mathcal{T}}$ uniformly at random from $\mathbb{F}$ subject to $s=\sum_{T\in\mathcal{T}} r_T$ (obtain a $k$-out-of-$k$ additive secret sharing of $s$). Let $s_i$ be the vector $s_i=( r_T )_{T\not\owns i}$.
- $\mathsf{Recon}$. Let $A\in \Gamma$ be a qualified set. Together, the parties in $A$ will hold all shares $\lbrace r_T\rbrace_{T\in \mathcal{T}}$ and can reconstruct the secret by $s=\sum_{T\in\mathcal{T}} r_T$.
Security is given since any maximally unqualified set $T$ will miss exactly one additive share, namely $r_T$. Correctness is ensured because any qualified set $A\in\Gamma$ cannot be contained in any unqualified set (due to the monotonicity of $\Gamma$) so parties in $A$ must jointly have all shares $r_T$.
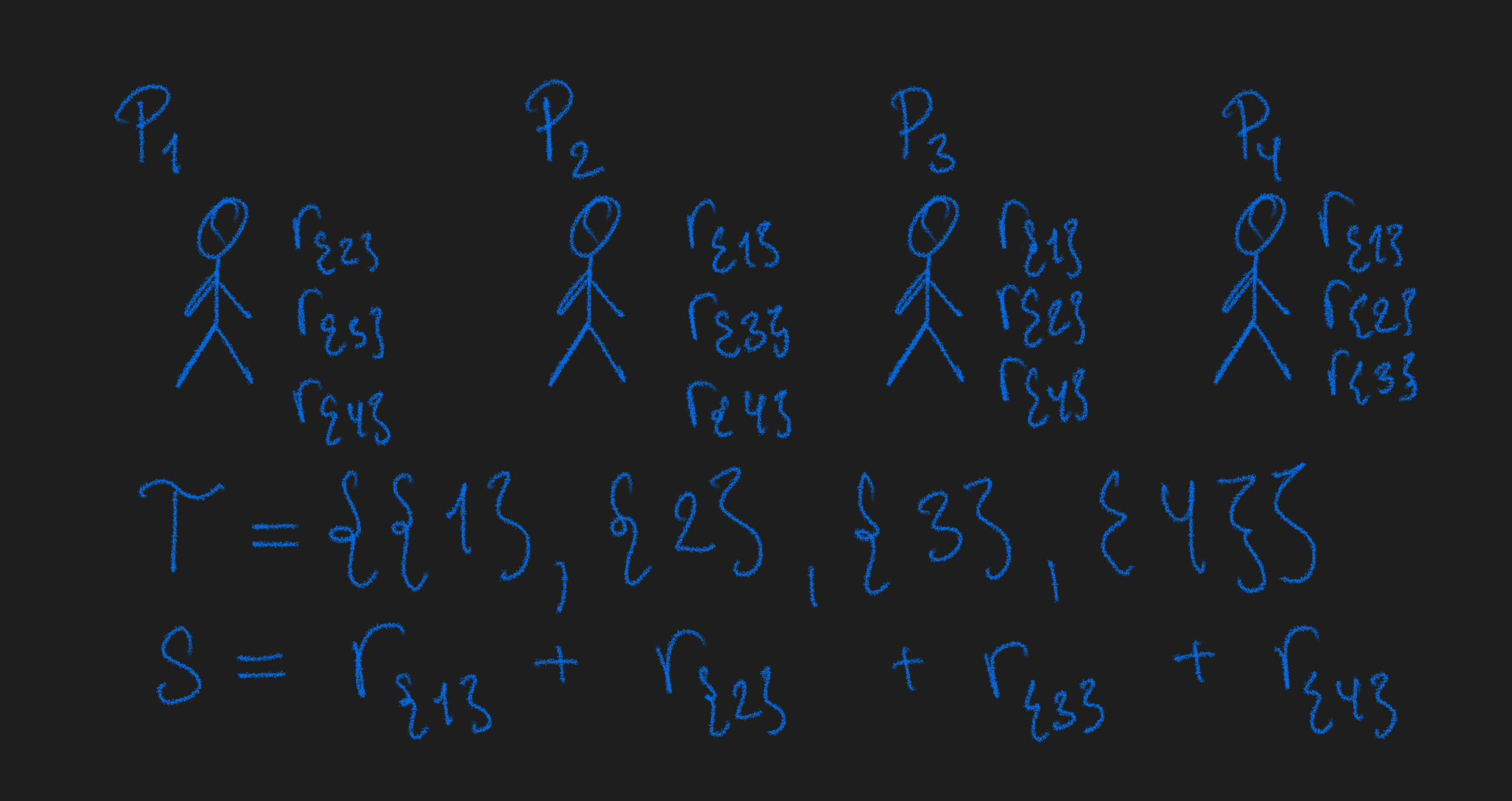
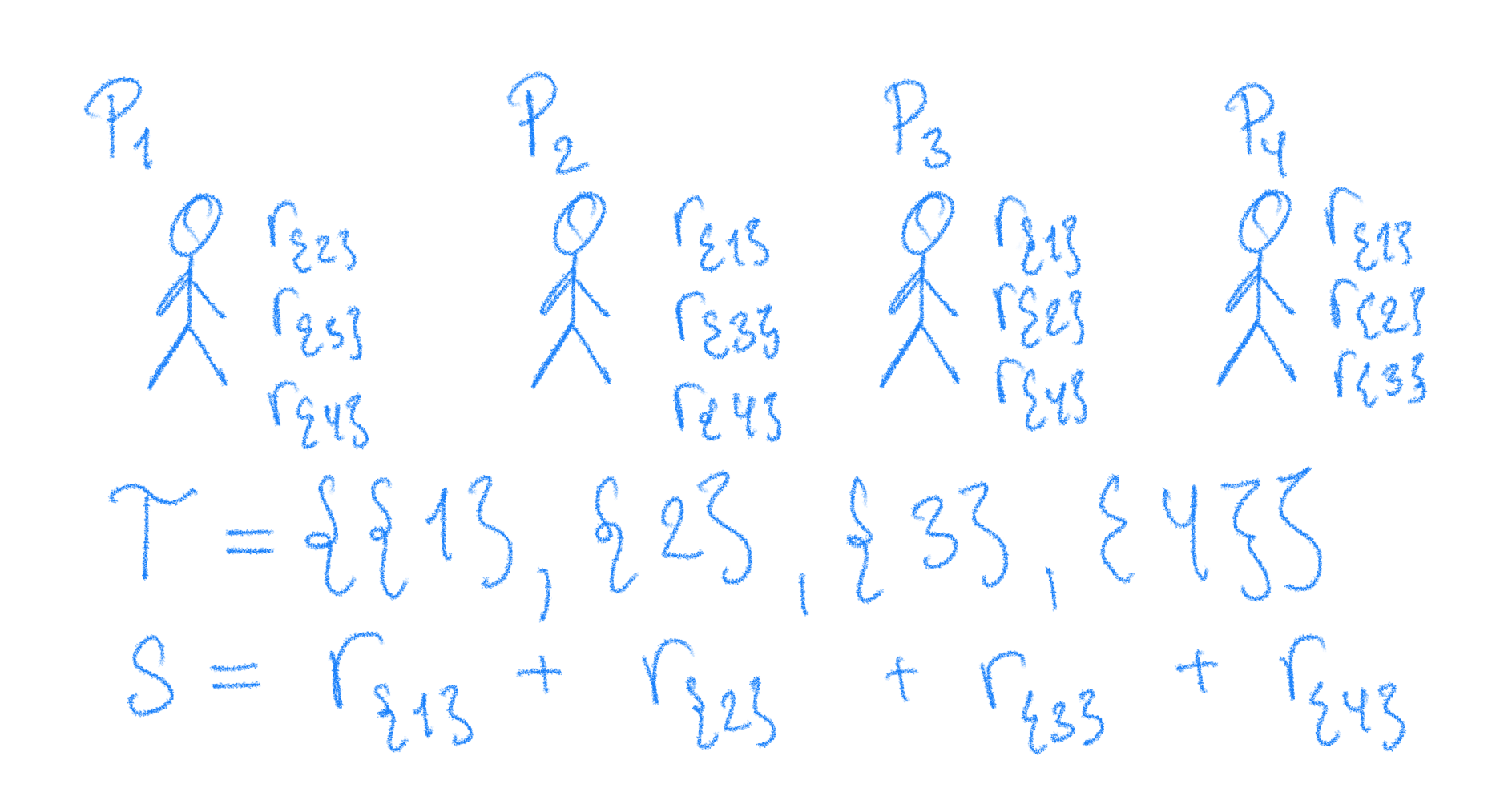CNF-Secret Sharing for access structure $\Gamma_{1,4}$
Conclusion
So, we have covered the basics of secret sharing. We got to know the most common secret sharing schemes; Shamir’s and CNF secret sharing. We got a feeling of how a question such as:
“Does a cruel access structure $\Gamma_{\mathsf{evil}}$ for $n$ parties exist, such that every secret sharing scheme has to distribute shares of exponential size in $n$?”
is deeply related to complexity theoretic concepts like Monotone Span Programs. However, we only scratched the surface. We did not even get into the relation between Shamir’s secret sharing and Reed-Solomon codes or the relation between ideal access structures with efficient LSSS and mathematical objects called matroids (read more here).
Oded Goldreich has chosen to focus on current and impactful (although) lesser known works within cryptography/complexity theory. My intention is to focus on techniques/papers that are close to my field of research and where I can extract small nuggets of wisdom as opposed to doing a full paper review. ↩
This is somewhat of a misnomer since CNF circuits contain NOT-gates which are explicitly forbidden in monotone formulae since they compute a monotone function that decides if a set is in the access structure (qualified) or not (unqualified). ↩